SSAGES Features
String Method
Within the elastic band method, the top level construct, a
string defining a path between two sites in free energy space,
is decomposed into a set of individual nodes which perform
short umbrella sampling calculations using a set of parallel
molecular dynamics and Monte Carlo calculations. At the end of
a data-gathering run, the position of the node in free-energy
space is updated, and through communication with neighboring
elements, the path is redefined. The figure at right presents a
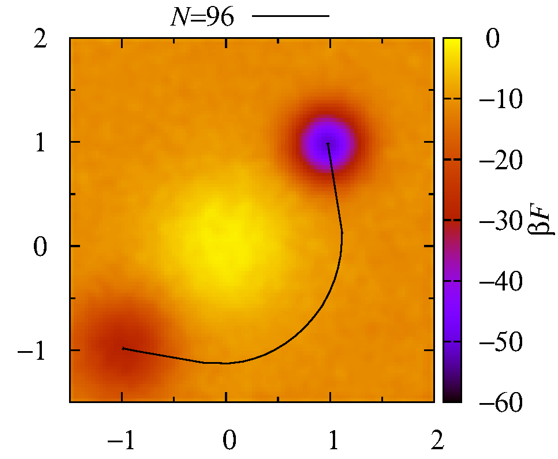
simple validation of the metadynamics and elastic band method
codes in SAGES suite. The heat-map is generated using
metadynamics performed on a single particle within a two
dimensional field containing three Gaussian potentials, one
peak and two wells. The minimum free-energy pathway between the
wells is obtained through evolution of a string with 96 nodes.
The system in this case evolves until only minimal driving
forces from the underlying FES remain; extended simulation
would push the elastic band out to hug the bounding
surface.
COPSS Features
General-geometry Ewald-like Method
The scheme provided by the General geometry Ewald-like
Method (GgEM) is a platform for multi-scale problems in physics
and chemistry. Applied to hydrodynamic equations, the method
solves for the proper behavior (both Brownian and Hydrodynamic)
of discrete entities such as polymers, cells and colloids, in
continuous fluid media. The Navier-Stokes equations are solved
using a Green's function approach for long-range interactions.
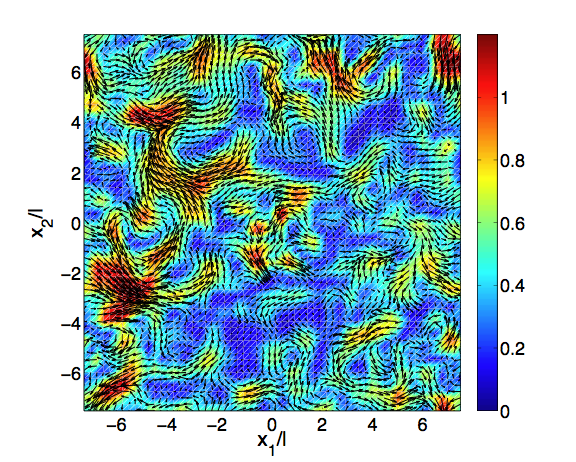
At right is a demonstration of GGEM methods applied to the
resolution of flow fields in suspensions of self-motile
particles.
Fast Multipole Boundary-element Method
The Fast Multipole Boundary Element Method (FMBEM) is a
code framework for various integral problems encountered in
scientific and engineering communities. It runs in parallel and
utilizes iterative solver GMRES accelerated by a
kernel-independent Fast Multipole Method (FMM) with O(N)
computational complexity. It applies to electrostatic
polarization problem involving arbitrary-shaped polarizable
dielectric objects embedded in a dielectric continuum, and also
to the calculation of interactions between
ferromagnetic/ferroelectric objects with arbitrary shapes. The
code is being developed using libMesh (finite-element library)
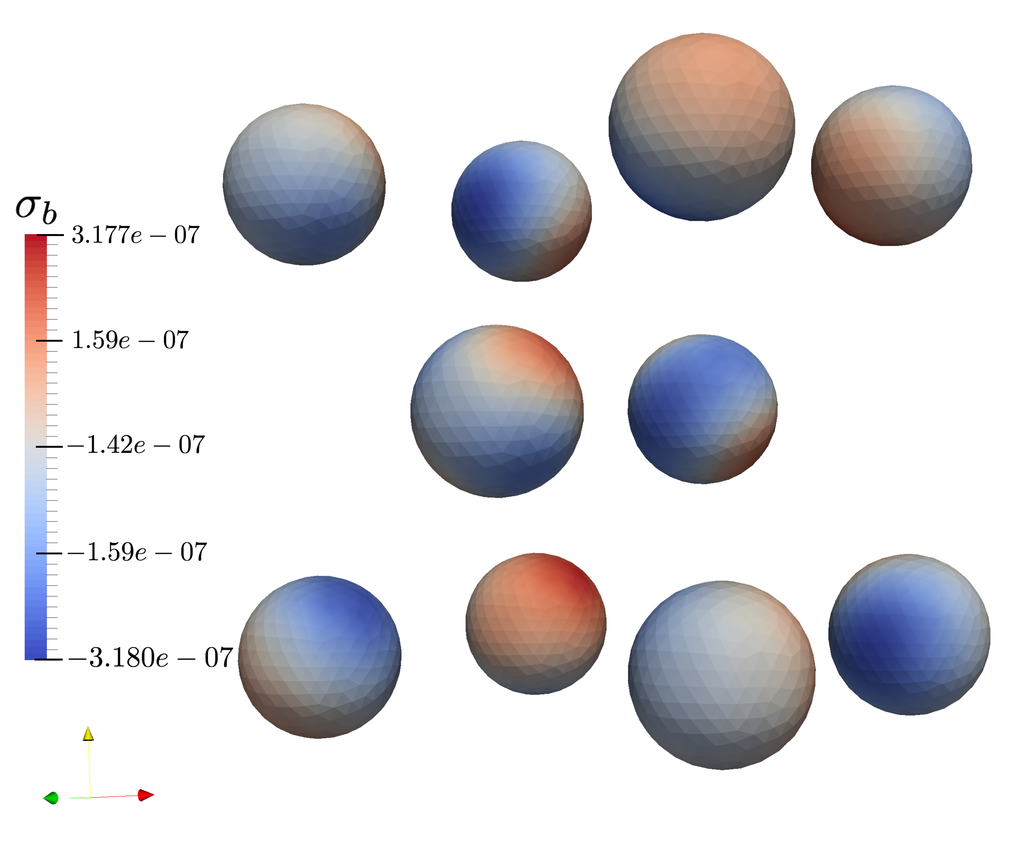
and ScalFMM (FMM library). At right is a demonstration of the
FMBEM applied to the electrostatic polarization problem among
interacting polarizable particles.
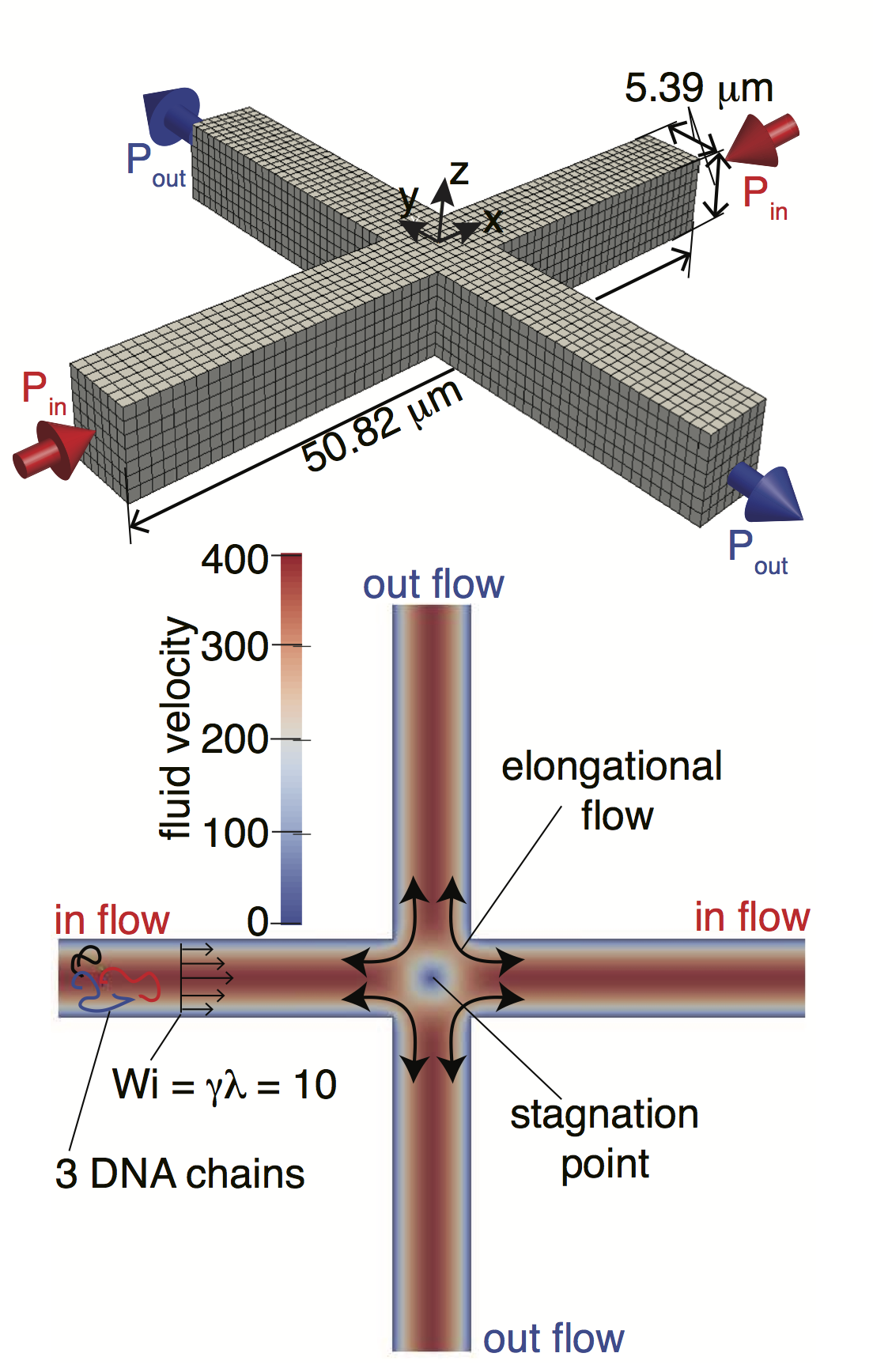
Parallel Finite-Element General-Geometry Ewald-like Method (pFE-GgEm)
Parallel finite element general geometry Ewald-like method (pFE-GgEm) is an efficient O(N) and
fully scalable computation framework to model the dynamics of Brownian particles considering
long-range hydrodynamic interactions (HI) in any geometries. The framework combines a FEM Stokes’
solver with GgEm, a mid-point integration scheme, and a Chebyshev polynomial approximation based
on the fluctuation-dissipation theorem. It is built on open-source scientific packages, such as
LIBMESH (framework of solving PDEs), PETSC (parallel linear, non-linear equation solver) and SLEPC (eigenvalue calculations).
At right is a demonstration of the pFE-GgEm applied to study the behaviors of DNA chains under
an elongational flow within a cross-channel geometry.